Recently one of my colleagues at my firm asked for my thoughts on a problem one of our clients was facing. Our client had recently been informed that their pension was shutting down and they had to decide on how to be paid out. They were given two options:
- Lump Sum: Receive $138,000 today of qualified money (not taxable until withdrawals are made in retirement), or
- Annuity: Receive $1,800 a month for life starting 17 years from today (this is when our client would reach age 62)
While a situation like this might never occur for you, deciding between a lump sum and an annuity is common for many people with pensions who are approaching retirement. So, what should our 45 year-old client do?
If you’re a numbers fiend like me (note: I’ve been referred to as Nicky Numbers at work), then your first instinct will be to value the Annuity. How much is $1,800 a month for life worth 17 years from now?
To do this we need to estimate: (1) how long our client live will past age 62 (when they start getting the Annuity) and (2) what return will they get on their money in retirement.
For life expectancy, we assumed that if our client made it to age 62 she would live 23 more years to be 85 (this comes from this actuarial life table from the Social Security Administration). For the rate of return, we conservatively assumed 5% annually on a 60/40 portfolio (with stocks earning 7% and bonds earning 2%).
Putting this all together, at the moment our client retires at age 62 their $1,800 monthly payments (or $21,600 annually) for 23 years (while earning 5%) would be worth ~$306,000 (assume annual payment at year start).
Great now, we have to compare this Annuity amount ($306,000) with what we would expect the Lump Sum to grow to by the time our client retires 17 years from today. The Lump Sum ($138,000), if compounded at 5% for 17 years would grow into ~$316,000.
This is a good check on our math as both the Annuity and Lump Sum tend to be actuarially similar with a 5% growth rate and an appropriate life expectancy.
Visually you can compare the Lump Sum to the Annuity by looking at how they both grow and draw down before and after our client’s retirement at age 62 [Note: the vertical line is when our client starts taking annual withdrawals of $21,600 in retirement]:
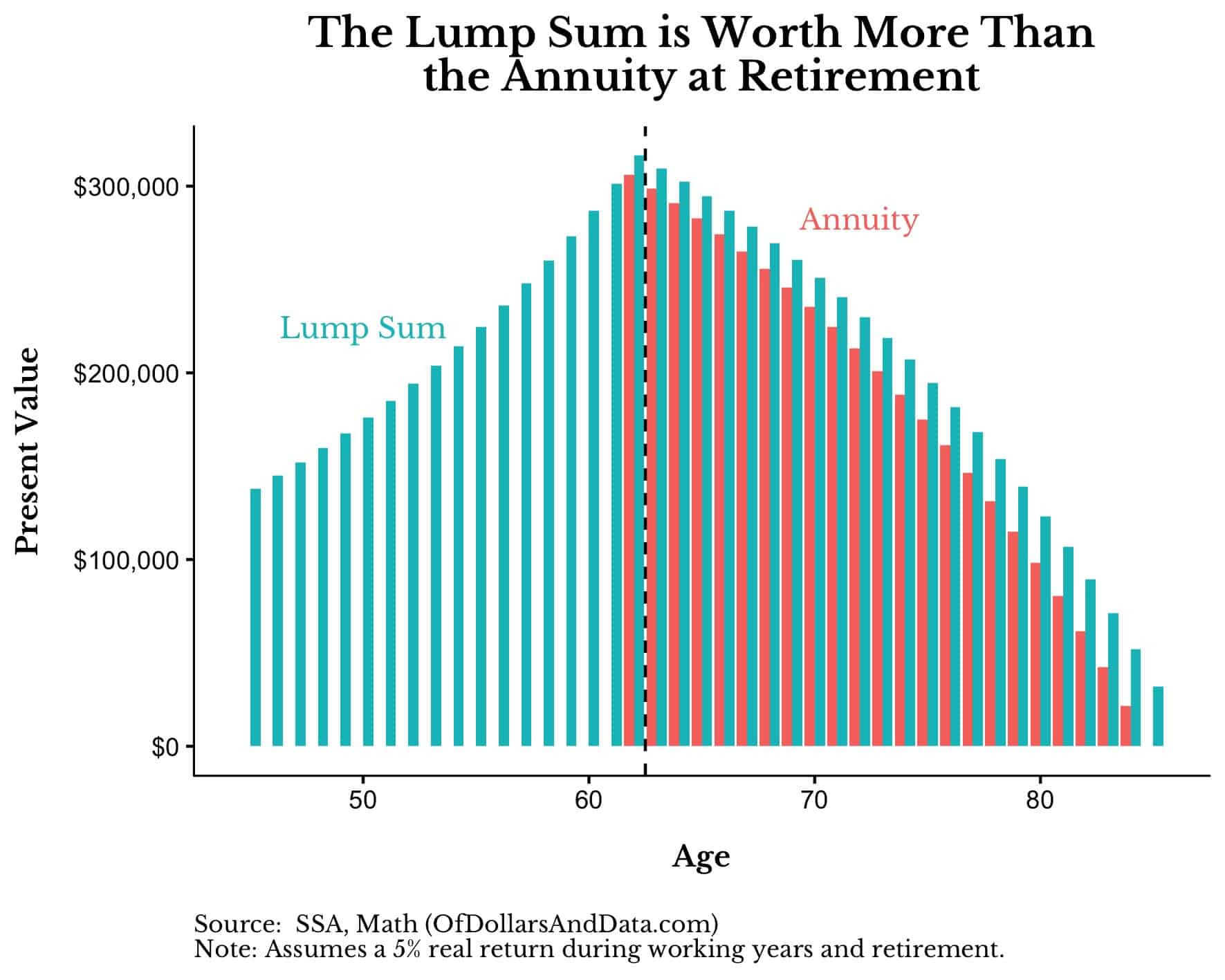
So, we tell our client to take the Lump Sum, right?
Not so fast. The Lump Sum has a problem. If you assume the same spending rate as the Annuity, the Lump Sum would run out of money before our client turns 87. This is not an issue for the Annuity which makes payments for life.
So, we have to ask, what is the probability that our 45 year-old client makes it to age 87 and beyond? Using the SSA life tables, there is a 43% chance that our client outlives what the Lump Sum would provide (all else equal). And if our client lives to age 62, the probability that she lives past age 87 is 46%.
More importantly, if our client makes it to age 87, her life expectancy is another 6 years.
If we re-run our simulation with a life expectancy of 87, you can see that the Annuity is now worth more than the Lump Sum:
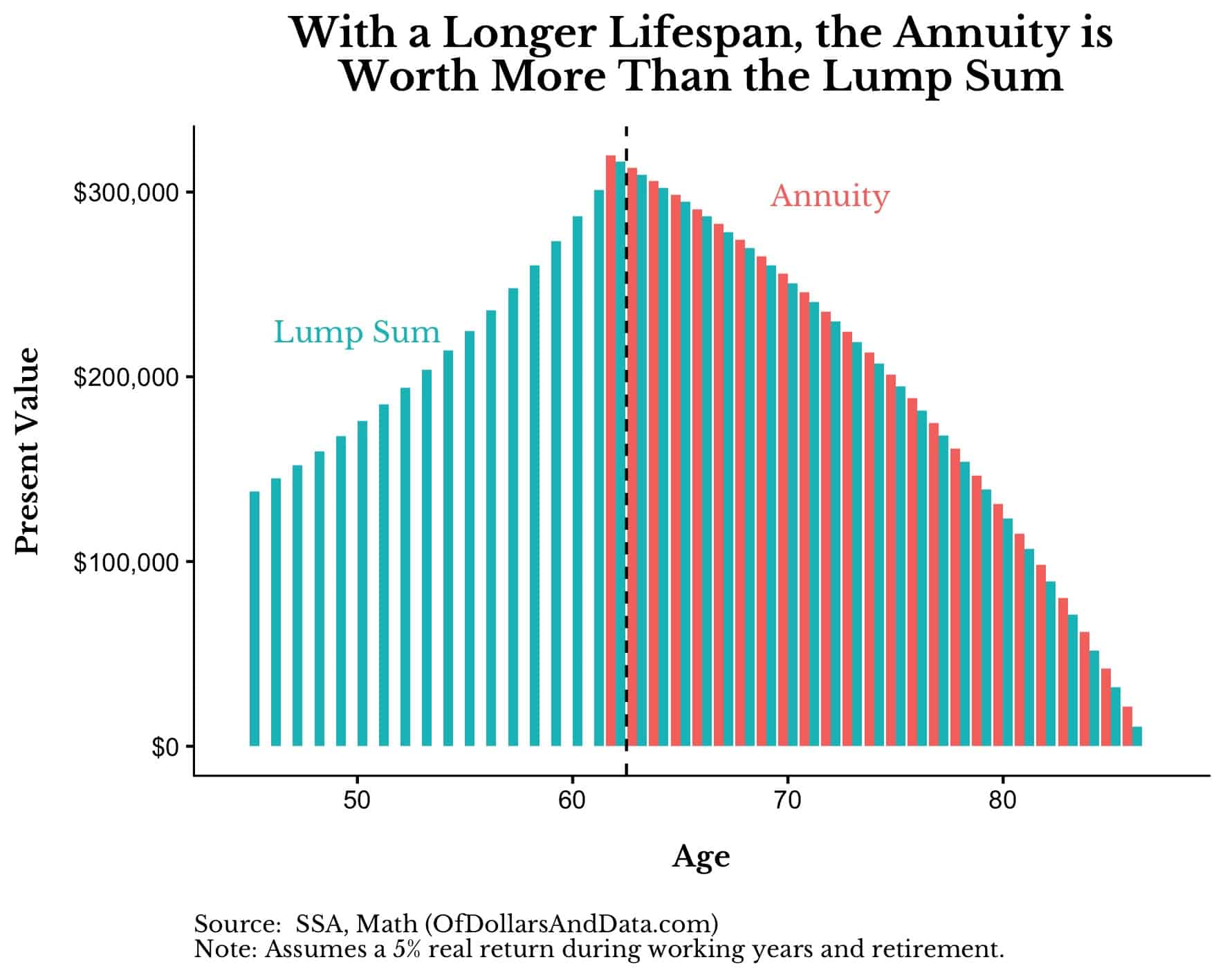
So the Annuity wins then right?
Well, not exactly. What if our client dies before they reach age 62? According to the SSA actuary tables, there is a 7% chance that this will occur, leaving our client’s heirs with nothing [Note: This assumes our client chooses a single life annuity option and not a joint life annuity option with a lower future payout].
So, with the 7% chance of dying early, but a 43% chance of outliving the money, our client should obviously take the Annuity, right? Not necessarily.
The one thing that the Lump Sum offers that the Annuity doesn’t is optionality. With the Lump Sum, our client would have a choice in how to invest, spend, and bequest their money.
This flexibility would allow our client to spend more in the early years of their retirement when they are in better health than they will be in later years. The Lump Sum also provides more flexibility with tax planning compared to the Annuity since it can be rolled into an IRA or other qualified retirement plan.
In addition, the Lump Sum would not have limits on the upside. Since a 60/40 portfolio has returned 9% historically, it is not out of the question for it to return 6% over the next 17 years and provide far more income in retirement than the Annuity.
But all of these questions come down to making tradeoffs. The question you have to consider when choosing between an Annuity and a Lump Sum is: What risk do you want to take?
- With the Lump Sum there is the risk of outliving your money either due to long life or subpar investment returns.
- With the Annuity there is the risk of dying before retirement age and the risk of seeing your income lose its purchasing power due to inflation.
In the end, we told our client to go with the Lump Sum because of the combined flexibility and the belief that it would outperform 5% annually. Given that a 60/40 portfolio has returned 6.5% over the last 5 years and 8% since the early 1990s, this assumption seemed reasonable.
I Can’t Get No Satisfaction
When it comes to the Lump Sum vs. Annuity decision, as I mentioned above, it all comes down what risks you want to take. I can understand how unsatisfying this answer is for those looking for a silver bullet. But if you approach retirement looking for the perfect solution, you won’t get it. Why?
Because as William Sharpe, the Nobel Laureate, notes, retirement is the “nastiest, hardest problem in finance.” And I agree. With the multiple layers of uncertainty (inflation, life expectancy, returns, and lifestyle choices) the problem is not solvable in the strict sense.
There is always risk that you cannot eliminate. There are things that are beyond all expectations. As the famous phrase goes:
Man plans, God laughs
Special thanks to Gary Pulford and Dan LaRosa for providing inspiration for this post and thank you for reading!
If you liked this post, consider signing up for my newsletter.
This is post 131. Any code I have related to this post can be found here with the same numbering: https://github.com/nmaggiulli/of-dollars-and-data

