It was January 1969 when the Department of Justice filed antitrust charges against IBM for monopolizing the computer market. Little did they know, the case would drag on for 13 years, cost the Department of Justice $15 million, and result in 2,500 depositions and over 60 million pages of documents. The charges against IBM were eventually dismissed in many ways because of the incredible work done by Cravath, Swain, & Moore LLP, the legal counsel hired by IBM.
The intriguing part of the story revolves around how Cravath defended IBM. Cravath’s strategy was complex and involved brute force — they wanted to win by outworking their opponents. In What it Takes, Charles Ellis highlights one such instance of Cravath employing this tenacious strategy:
[They had] organized over a dozen Cravath lawyers there in a pattern of 8:00 A.M. to 2:00 A.M. workdays. Every day throughout the trial, the day’s transcript was obtained at about 10:00 P.M. by a team of Cravath lawyers, who took it apart and reorganized the contents into proposed findings of fact to support the series of propositions Cravath sought to prove for IBM. Each was cross-referenced to specific pages in the original transcript.
Max Blecher, a lead plaintiff attorney working against Cravath, said he was “stunned by the enormous effort expended on a simple motion to dismiss.” Blecher continued (emphasis mine):
The sheer manpower that took — the cost — I just felt overwhelmed. I often wondered how they could operate if the client imposed any cost control at all. Everything showed this attitude. They buried us in paper. They produced reams of paper in futile endeavors…We stacked up the paper — it was five or six feet tall!
Cravath’s ability to win was based upon overwhelming effort — it was success by exhaustion.
Scott Galloway, the famed marketing professor at NYU, describes how this method has worked in other domains as well:
The majority of (actual) wars have not been won with strategy, bravery, training, or superior equipment, but brute force. At the end of WWII, the Allies had 38 gallons of gasoline for every one the Germans did. Amazon is the retailer with 38 gallons.
And Amazon uses those “38 gallons” to great effect by regularly experimenting in new lines of business though these experiments will likely produce no profits (or negative profits) for the first 5–7 years. There is a similar story about how Thomas Edison and his team tested more than 6,000 different materials before finding the right one for the lightbulb. In both cases, exhausting all possibilities became a formula for success.
My point is that many of the greatest wins in history came as a result of brute force. Given this observation, there are a few ways that you can utilize this kind of approach to improve your finances:
- Use indexing to solve the problem of stock picking
If you think about it, indexing is a brute force solution of the problem of picking stocks. It is difficult to know which stocks will do well and which ones won’t, so your best bet is to buy them all and hope the aggregate return is positive. You can extend this idea across asset classes as well by diversifying your portfolio.
- Increase your savings rate to make your investment returns less important
Saving more money is a brute force solution to the problem of unknown future investment returns. For example, if you assume a 10% return, you may only need to save $X in order to retire. However, if you don’t get 10% every year you will be in trouble…unless you can save more money. At the extreme, if you can save enough money you won’t need any returns (assuming you can keep pace with inflation).
Consider how many years it would take to save for retirement as you increase your savings rate. To go through this thought experiment we will assume that you save the same amount of your after-tax income annually and it grows at some constant rate annually. We will also assume that you can stop saving (i.e. you can retire) once the return on your total savings is the same as the after-tax income you live off of. Basically, you would live off of the interest and your principal balance would stay constant in retirement.
For example, if you make $100,000 after-tax annually and save 20%, this means you live on 80% ($80,000). If we assume a 10% annualized return, it would take a little under 20 years to be retired. If we assume a 4% annualized return, it would take closer to 45 years to be retired. Below is a graph showing how many years it would take to retire given some savings rate (x-axis) and annual return (different colored lines):
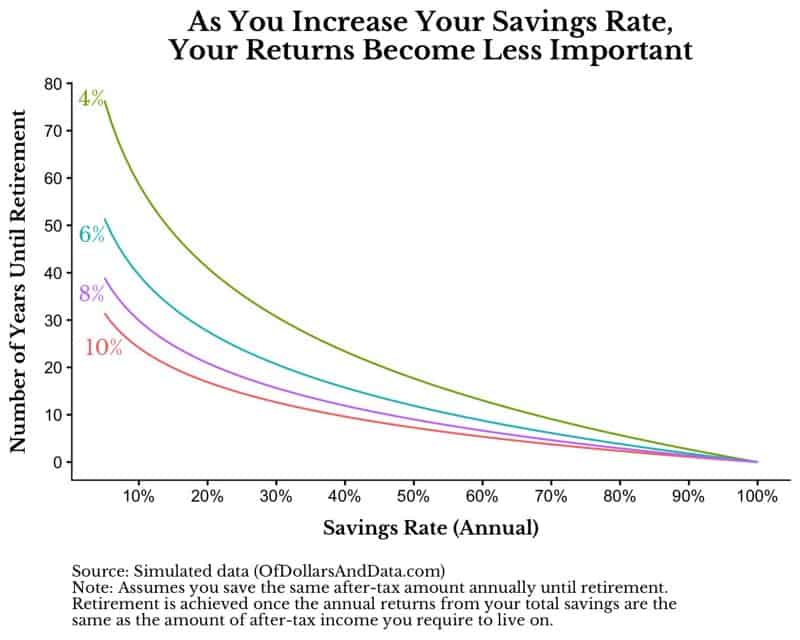
As you can see, as the savings rate increases, the number of years you need to work until retirement decreases drastically. I first heard of this idea from Mr. Money Mustache (here). More importantly though, there is a convergence between the different annual return lines as the savings rate increases. Why? The more money you save, the less important your returns are for reaching your goals. This is an amazing result, because it shows how you can succeed in almost any market environment, if you are able to save enough.
Success by Exhaustion Outside of Finance
Though Of Dollars And Data is an investment/finance blog, there are many times where I discuss ideas that are not directly related to finance. I do this because investing is primarily a behavioral exercise, and if I can get you to understand your behavior, you are far more likely to be a successful investor.
So where can you apply this idea outside of your personal finances? You can apply it to your career, your health, your side projects, and so much more. By working hard and finding what works best for you through brute force, you can drastically change your life.
If you are interested in how this approach can be used in your career, I highly recommend What It Takes by Charles Ellis. That book inspired me to work harder than I thought possible and made me more than a 1000x return on the purchase price of the book. I can only hope that you find it as useful as I did. Thank you for reading!
If you liked this post, consider signing up for my newsletter.
This is post 56. Any code I have related to this post can be found here with the same numbering: https://github.com/nmaggiulli/of-dollars-and-data

