Imagine that you just received a raise at work and are tempted to go out and celebrate. After all, you’ve worked hard and you deserve something nice, right? Maybe you want a new luxury car? A better place to live? Or, maybe, you just want to dine out more often?
No matter what you decide to do with your newfound cash, you’ve just fallen victim to lifestyle creep. Lifestyle creep is when someone increases their spending after experiencing an increase in income. So that new raise quickly becomes a fancy new object or an expensive new habit, and, before you know it, your raise is gone.
For this reason, many personal finance experts will tell you to avoid lifestyle creep at all costs. However, I am not one of them. In fact, I believe that some lifestyle creep can be very satisfying. After all, what’s the point of working so hard if you can’t enjoy the fruits of your labor?
However, there is a limit to how much your spending can increase before it begins to affect your financial future. Where is that limit? Technically, it varies based on your savings rate (we’ll get into that later), but, for most people, the limit is around 50%. Once you spend more than 50% of your future raises, then you start delaying your retirement.
It might seem odd that earning extra money could force you to delay your retirement, but it all depends on how much of that extra money you spend. More importantly, I’ve found that people with higher savings rates need to save a larger percentage of their future raises than people with lower savings rates, all else equal.
In this blog post, I will:
- Explain why those with higher savings rates need to save a larger percentage of their future raises
- Quantify how much of your future raise you should save (based on your current savings rate)
- Argue why saving 50% of your future raises is the sweet spot.
Let’s begin.
Why High Savers Need to Save More of Their Raises
To start, let’s imagine two different investors: Annie and Bobby. Both of them earn the same after-tax income of $100,000 a year, however, they save different amounts annually. Annie saves 50% of her after-tax income ($50,000) each year, while Bobby only saves 10% ($10,000). By definition, this means that Annie spends $50,000 and Bobby spends $90,000 a year.
If we assume that Annie and Bobby both want to spend the same amount of money in retirement as they did while working (i.e. lifestyle maintenance), then Annie will require less money to retire than Bobby. If we also assume that each investor needs 25x of their annual spending to retire comfortably, then Annie requires $1.25M, while Bobby will require $2.25M to retire. With a 4% real rate of return and no changes in their income/savings rates over time, Annie will be able to retire in 18 years while Bobby will take 59 years.
Now, let’s go 10 years into the future. After 10 years of saving (with a 4% inflation-adjusted return), Annie will have accumulated $600,305 while Bobby will have $120,061. They are both still on track to retire on their original schedules (i.e. Annie in 8 years and Bobby in 49 years).
But, now let’s say they both get a raise of $100,000 a year to increase their earnings to $200,000 annually (after-tax). How much of this raise should Annie and Bobby save if they want to retire on their original schedule? You might think, “Just save at their original savings rate,” right? But if Annie saves 50% of her raise and Bobby saves 10% of his raise, this would actually delay their retirements.
Why? Because their retirement goal hasn’t accounted for their increase in spending as a result of their raise. If Annie is now making $200,000 a year and saving 50% of it ($100,000), by definition, she is spending the other 50% of it ($100,000) each year as well. Since her spending doubled from $50,000 to $100,000 a year, her spending in retirement must double if Annie wants to maintain her new $100,000 a year lifestyle.
This means that Annie now requires $2.5M to retire instead of her original $1.25M. However, because Annie saved for 10 years as if she only needed $1.25M for retirement, she must now work longer to make up for this lower level of savings in her past.
With $600,305 invested and annual savings of $100,000 (at a 4% rate of return), Annie would reach her $2.5M retirement goal 12.2 years from now instead of her original plan to retire 8 years from now. Her lifestyle creep pushed back her retirement date.
If Annie wanted to retire on her original schedule, she would have to save 74% of her $100,000 raise going forward. This means that Annie is now saving $124,000 a year ($50,000 original annual savings + $74,000 from the raise) until retirement. At this level of savings, Annie’s retirement target would be $1.9M and she would get to spend $76,000 a year in retirement. So, the raise improves her lifestyle and her retirement, but not as much as she might have initially imagined.
And what about Bobby? If he wanted to retire in 49 years after getting a $100,000 raise, he would need to save an additional $14,800 a year or 14.8% of his raise to do so. This gives him annual spending of $175,200, but still requires another 49 years for him to reach retirement. Obviously, saving for 59 years isn’t practical for most people, so Bobby will have to save much closer to the 50% guideline discussed earlier if he wants to retire within a more reasonable timeframe.
More importantly though, if Annie and Bobby want to retire on their original schedules, Bobby only has to save 14.8% of his raise while Annie has to save 74% of her raise. This is empirical proof that higher savers have to save an even larger percentage of their raises (compared to lower savers) if they want to keep their retirement date constant.
Now that we have looked at why higher saves need to save more for their future raises, let’s figure out how much of your future raises you should save.
How Much of Your Raise Should You Save?
Given the example above, the most important factor in determining how much of your raise you need to save (to have the same retirement date) is your current savings rate. Differences in annual rate of return, income level, and income growth rate matter far less for this discussion. And, yes I tested all of these things and savings rate was the most important.
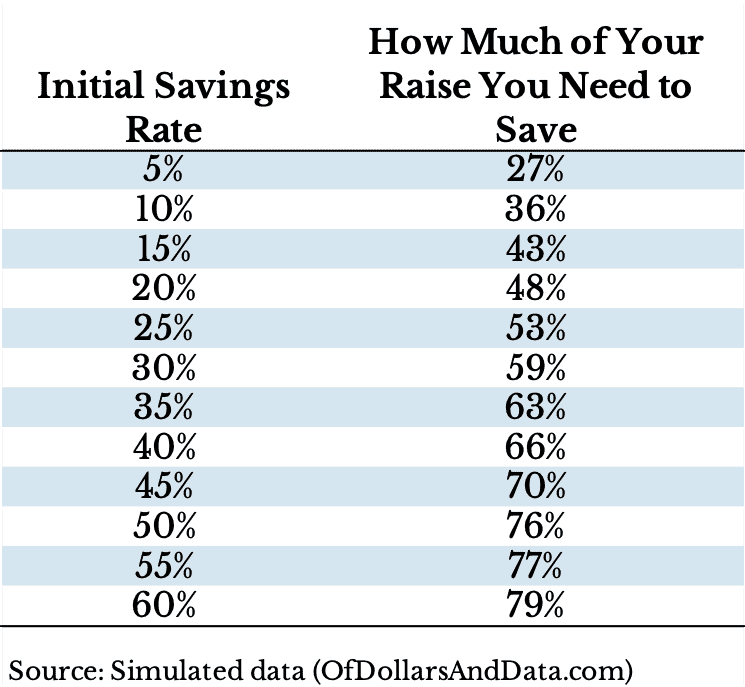
Therefore, below I have created a table showing how much of your raise you need to save to have the same retirement date based on your initial savings rate. This analysis assumes that you require 25 times your annual spending to retire, your income grows at 3% a year, and your portfolio grows at 4% a year (all in inflation-adjusted terms):
So, if you save 10% a year now and get a raise, then you need to save 36% of that raise (and 36% of all future raises) in order to retire on the same timetable. If you save 20% now, then you need to save 48% of your future raises. If you save 30% now, then you need to save 59% of your future raises, and so forth.
What this really shows is that some lifestyle creep is okay! For the person saving 20% of their income now, they are allowed to spend half of their future raises without altering their retirement timeline. Of course, if they spend less than half of their future raises, they can retire sooner, but that is up to them.
Counter-intuitively the lower your initial savings rate, the more your lifestyle can creep without affecting your current retirement plan.
Why? Because those people who save less, by definition, spend more (for the same level of income). Therefore, when these low savers get a raise and decide to spend a portion of it, it affects their total spending less than a higher saver who got the same raise and spent the same percentage of it. It is the impact of a raise on spending that disproportionately affects higher savers more than lower savers.
This is the core idea behind Mr. Money Mustache’s Shocking Simple Math to Early Retirement. As his post illustrates, your savings rate not only affects how much money you have now, but also how much money you will spend later. This same logic explains how not saving enough of a raise can delay your retirement.
Why You Should Save 50% of Your Raises
Despite all the complicated theory, assumptions, and analysis shown above, I suggest that you save 50% of your raises simply because this is what will work for most people most of the time. If we assume that the vast majority of savers have savings rates in the 10%-25% range, then the 50% limit is the correct solution based on my simulated data (see table above). And if your savings rate is currently below 10%, I can only assume that saving 50% (or more) of your future raises is in your best interest.
More importantly, saving 50% of your raises is easy to implement and remember. Half is for you and half is for future you (retirement). Coincidentally, this idea is similar to the 2x rule I wrote about in my book, Just Keep Buying, when discussing how to spend money without feeling guilty. As a quick refresher, the 2x rule states that before you buy something expensive, you need to set invest a similar amount of money buying income-producing assets. So if you want to spend $400 on a pair of nice dress shoes, you would also need to spend $400 on an S&P 500 index fund.
This is the equivalent of a 50% marginal savings rate and just so happens to perfectly fit with the 50% limit on lifestyle creep highlighted above. So go out and enjoy your raises, but remember, only half. With that being said, happy saving and thank you for reading!
If you liked this post, consider signing up for my newsletter.
This is post 205. Any code I have related to this post can be found here with the same numbering: https://github.com/nmaggiulli/of-dollars-and-data