My favorite fable as a child was Aesop’s The Tortoise and the Hare. For those that aren’t familiar, the story centers around a race between a fast, arrogant rabbit and his much slower, shelled counterpart. But what makes this race intriguing is that, after gaining a sizable lead, the hare decides to take a nap during the race, believing that his victory is all but assured.
Unfortunately, the hare wakes to find that the tortoise has passed him. Despite making a mad dash toward the finish line, the hare comes up short and loses the race.
While most people see the moral of the story as “don’t be overconfident” or “slow and steady wins the race,” I see it as a warning against terrible decision making. After all, it is the hare’s bad decisions and not the tortoise’s good decisions that lead to the hare’s defeat.
This is the same premise behind Winning the Loser’s Game by Charles Ellis. In the book, Ellis describes what he calls “winners’ games” and “losers’ games”:
In a winner’s game, the outcome is determined by the correct actions of the winner. In a loser’s game the outcome is determined by the mistakes made by the loser.
Ellis then goes on to explain how investing is a loser’s game, because most investors who attempt to beat the market (i.e. those who try to win) typically underperform in the long run. For example, using excessive leverage or paying high fees for expected outperformance are two common ways in which would-be winners become definite losers.
The better strategy for investors then is not to try and win, but to not lose. Too many people in the financial community (especially FinTwit) obsess over the “optimal” way to invest when their time would be better spent steering clear of actions that could lead to ruin.
Warren Buffett said it best in his 2005 Berkshire Hathaway letter to shareholders:
Over the years, a number of very smart people have learned the hard way that a long string of impressive numbers multiplied by a single zero always equals zero.
The warning from Ellis and Buffett alike is crystal clear: avoid the zeros. Avoid them at all costs.
Why? Because the zeros are those things that can set you back years or decades in an instant. What are “the zeros” exactly?
In the investment world, the zeros are usually things associated with high costs (i.e. fees, taxes, extravagant spending, etc.) or high risks (i.e. leverage, concentration, etc.). All of these things, if not managed properly, can wreak havoc on your finances.
But, avoiding negative financial outcomes also goes beyond your investment decisions.
For example, while many financial experts claim that your asset allocation or your savings rate are the most important financial decisions you will make in your life (they are quite important!), I’d argue that who you decide to marry will have a far bigger impact on your finances in the long run.
Why? Because what happens if you select the wrong spouse and end up going through a divorce?
In that case, it doesn’t matter how good your returns were or how high your Sharpe Ratio was, because any number multiplied by 0.5 will be disastrous for your portfolio!
But, avoiding the zeros isn’t just for your investment portfolio, it can also be applied to other parts of your life as well.
In his book Antifragile, Nassim Taleb refers to this approach as via negativa and thoroughly demonstrates the powerful health benefits associated with adhering to it:
For instance, telling people not to smoke seems to be the greatest medical contribution of the last sixty years. Durin Burch, in Taking the Medicine, writes:
“The harmful effects of smoking are roughly equivalent to the combined good ones of every medical intervention developed since the war. Getting rid of smoking provides more benefit than being able to cure people of every type of cancer.”
As Taleb illustrates, avoiding negative behaviors has done more for individual health than the cumulative effective of many positive medical interventions.
Rather than apply this same framework to the many other facets of life, let me show you how this approach would work through simulation.
To start, imagine you have a choice between two assets to invest in:
- Asset A returns +4% in 99% of periods and -96% in 1% of periods. The expected return for this asset in one period is +3% [(0.99*0.04) + (0.01*-.96) = 0.03]
- Asset B returns +1% in all periods.
Which asset would you prefer to invest in? If you had to invest for 1 period only, most of you would likely pick Asset A, but what if you had to invest for 100 periods or 1,000 periods?
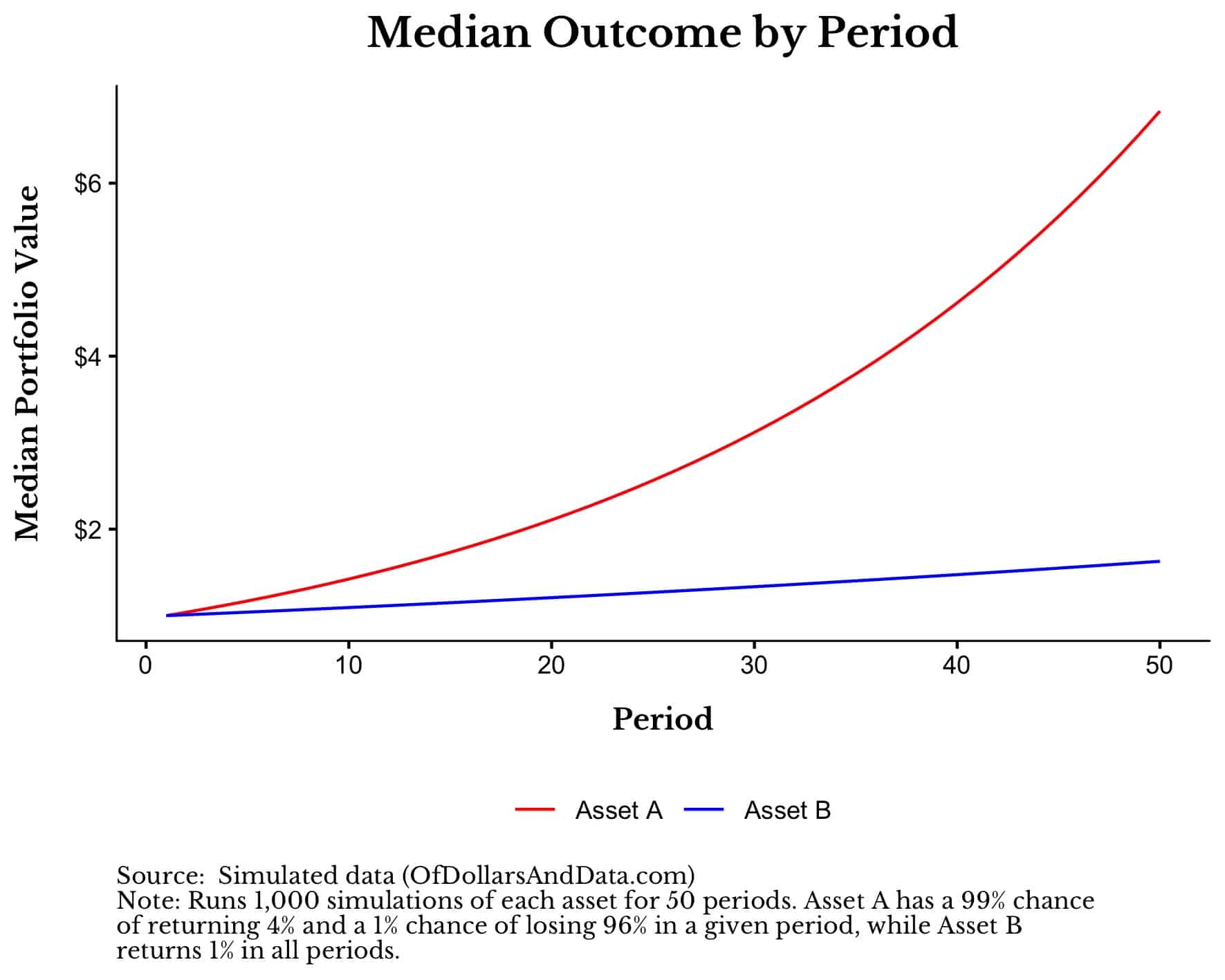
To test this, I ran 1,000 simulations of each asset assuming you invested $1 into each. Here are the results for the median simulation across the first 50 periods:
As you can see, Asset A completely dominates Asset B because a majority of the simulations have not experienced their 96% loss…yet.
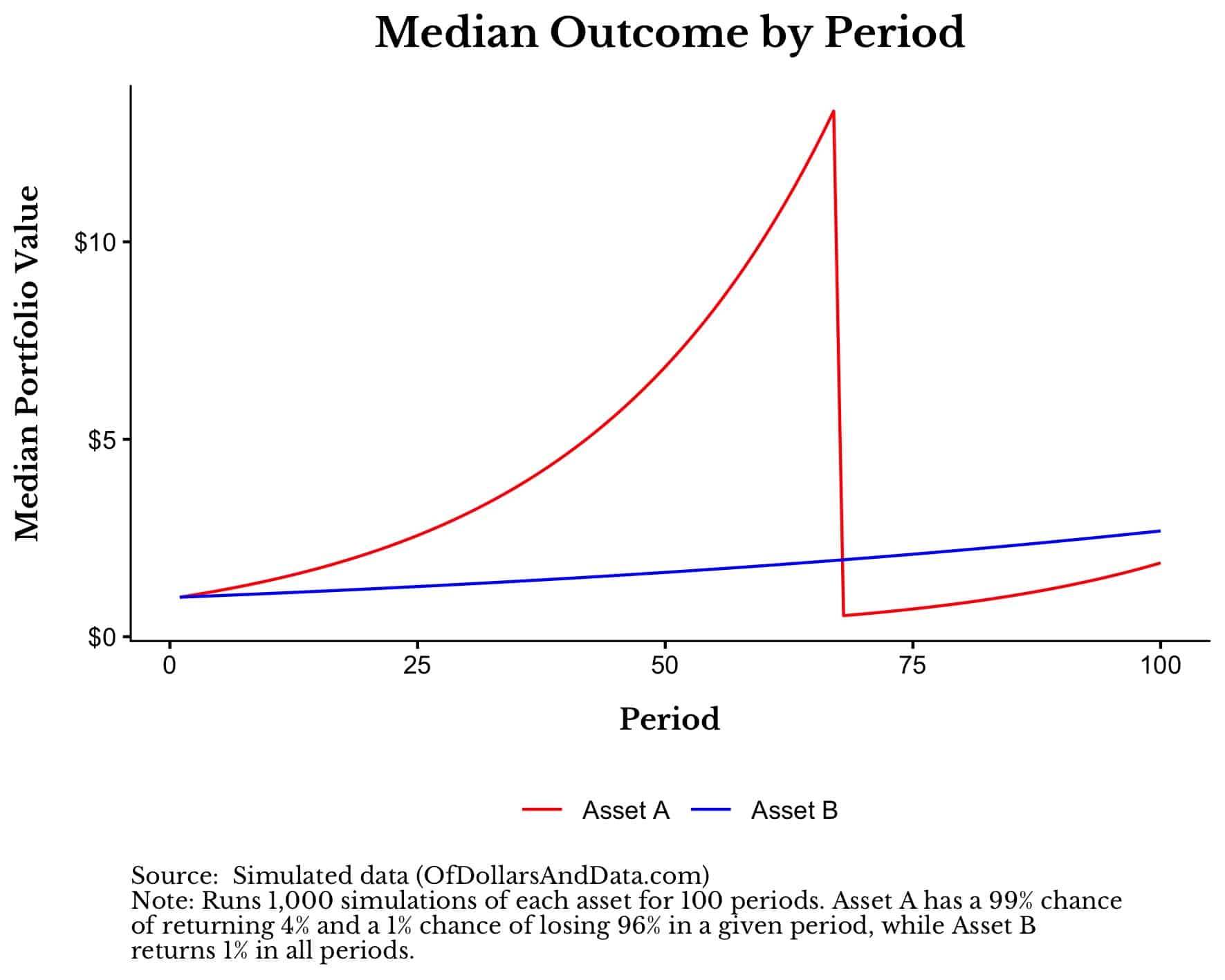
But, if we extend this simulation out to the first 100 periods, you will notice that the results aren’t quite the same:
Now Asset B leads Asset A (starting around the 70th period) as over half of the simulations (i.e. including the median simulation) have experienced their 96% loss. But what happens if we keep going?
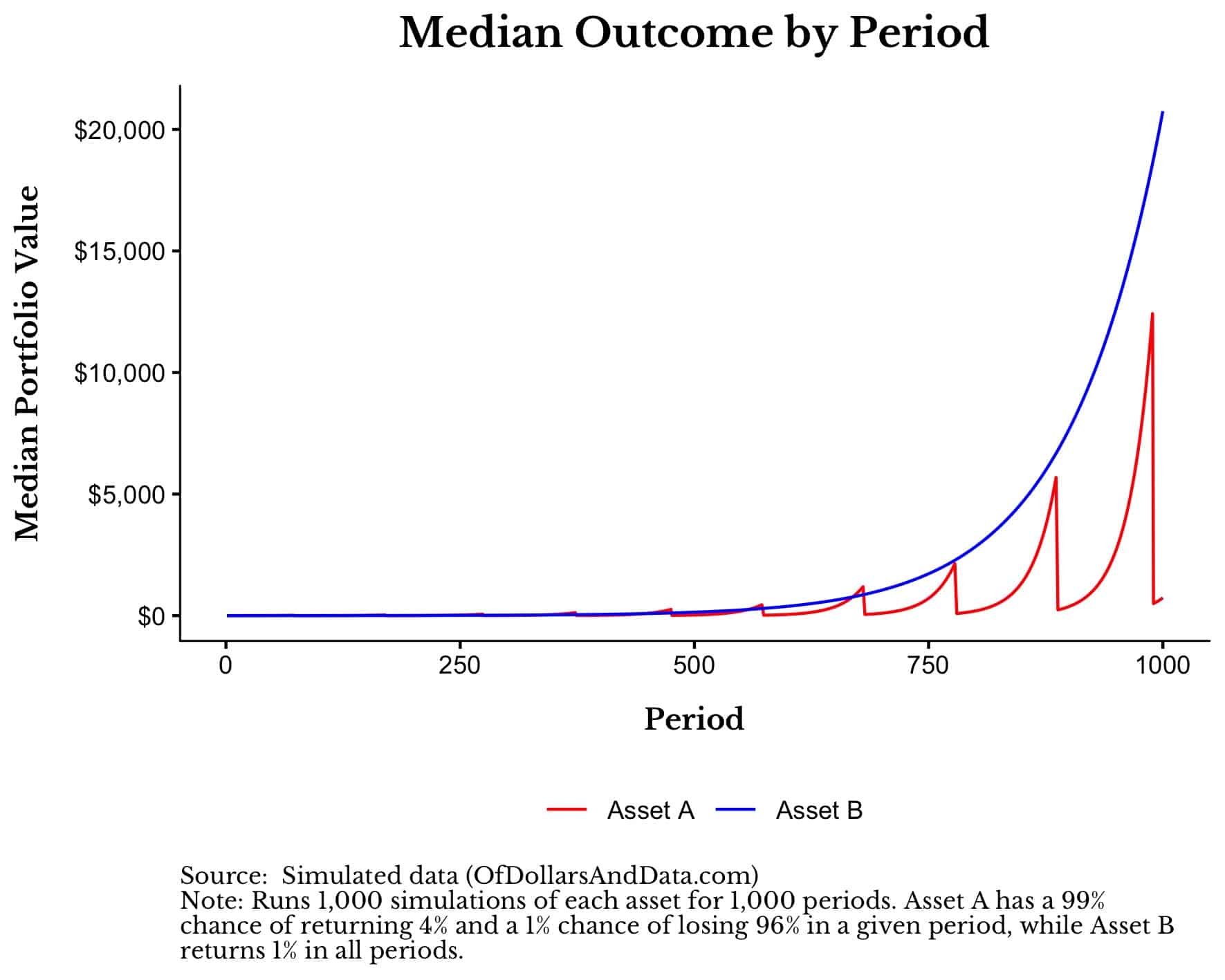
At 1,000 periods, one of the assets begins to permanently pull away from the other:
Why does this happen? Because though Asset A has higher returns than Asset B in most periods (4% > 1%), Asset A also has catastrophic returns in some periods that it cannot make up for in the long run.
Asset B performs better because it “avoids the zeros” (the large, infrequent losses) unlike Asset A.
You might be wondering how it’s possible that Asset A underperforms Asset B for the majority of the simulations despite having a higher expected return.
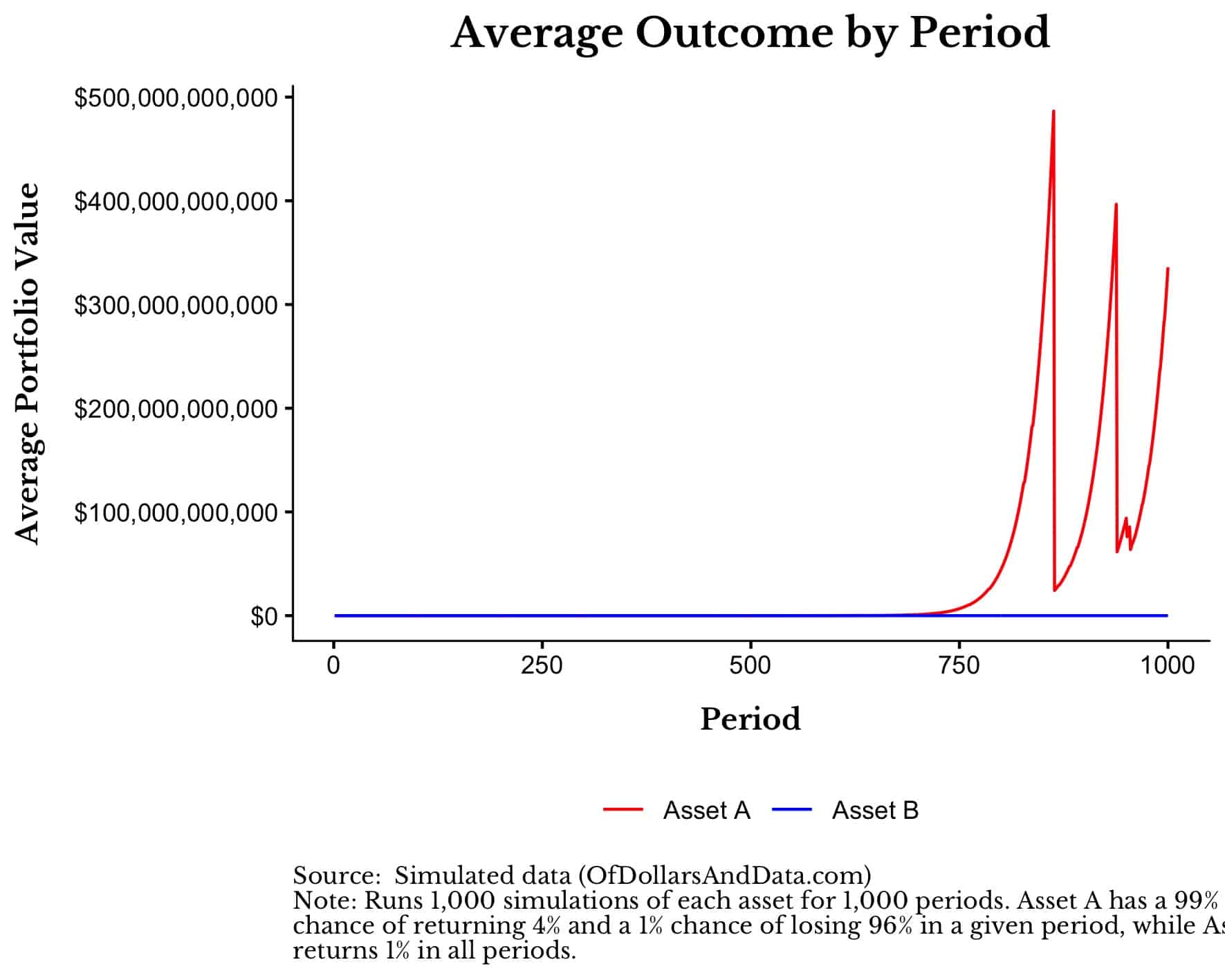
While this is true in the median simulation, this is not necessarily true if we take the average across all simulations.
When we take the average, Asset A easily outperforms Asset B since a smaller number of simulations of Asset A experience few (if any) 96% losses across 1,000 periods. Those few lucky simulations would completely skew the average in favor of Asset A over Asset B.
For example, just look at how ridiculous the results become when using the average outcome across all simulations for the first 1,000 periods:
In this instance, Asset A clearly dominates though only due to luck. You can imagine how someone might market Asset A without disclosing that this is the result of chance.
But, you don’t have to imagine because that is exactly what many “zero” investment strategies do. They ignore all the losers and market the winners to unsuspecting victims. They have to do this.
Because no one in their right mind would hand over their money to these financial charlatans if they saw all the zeros.
Avoiding the Zeros as a Lifestyle Choice
I used to think that my edge in life was being smart, but it really isn’t. My edge is being not stupid. There’s a big difference.
For example, Myron Scholes, the Nobel prize winning economist, is far smarter than me, yet I have the better investment record. Anyone who knows about Scholes’ magnificent losses with Long Term Capital Management (LTCM) can attest to this.
How is it possible that a Nobel Prize winner can have a worst investment record than a typical investor like me? Because that Nobel Prize winner played a stupid game. In the case of Myron Scholes and LTCM, that stupid game was called leverage.
How do I know it was stupid? Because if Warren Buffett only levered 1.6-to-1 throughout his career, why would you ever go beyond this limit, let alone 50x over it, as LTCM often did?
As the saying goes, “Play stupid games, win stupid prizes.” So don’t play. Not even once.
When I look back upon my life I am quite proud of my general ability to be not stupid. This is why I gave up binge drinking last year. I realized that nearly all of the stupid decisions in my life came as a result of alcohol so I had to take a step back.
Of course, nothing says that I won’t act foolishly in the future. We all make mistakes after all. Let’s just hope that those mistakes aren’t zeros.
Thank you for reading!
If you liked this post, consider signing up for my newsletter.
This is post 163. Any code I have related to this post can be found here with the same numbering: https://github.com/nmaggiulli/of-dollars-and-data